Pembangkitan soliton otomatis menggunakan efek termo-optik negatif.
Penelitian
Pembangkitan soliton otomatis menggunakan efek termo-optik negatif.
Menuju aplikasi praktis dari com mobil optik
Sisir frekuensi optik, yang diperkenalkan oleh Hänsch dkk. pada tahun 1999, telah digunakan secara luas sebagai 'ukuran cahaya' dengan spektrum berbentuk sisir yang memungkinkan pengukuran frekuensi optik yang tepat. Teknologi ini memenangkan Hadiah Nobel Fisika pada tahun 2005 dan diadopsi sebagai standar nasional untuk panjang di Jepang pada tahun 2009. Dalam beberapa tahun terakhir, penelitian tentang carcom optik, di mana generator (resonator) sisir frekuensi optik diminiaturkan ke skala mikro dan hemat energi, telah aktif. Keadaan yang paling stabil dari sisir mobil optik disebut soliton optik, dan penelitian terdahulu telah menunjukkan bahwa keadaan ini dapat diperoleh dengan secara tepat mengubah panjang gelombang cahaya input relatif terhadap panjang gelombang resonansi. Namun demikian, terlepas dari kenyataan bahwa panjang gelombang resonansi dipengaruhi oleh panas yang dihasilkan oleh penyerapan dan faktor lainnya selama pembangkitan Kercomb optik yang sesungguhnya (efek termo-optik), hanya ada sedikit penelitian yang memperhitungkan efek panas.
Dalam penelitian ini, model komputasi baru dikembangkan untuk memperhitungkan efek termal dan, khususnya, metode pembangkitan soliton optik menggunakan efek termo-optik negatif, yang belum pernah dipertimbangkan sebelumnya, didemonstrasikan secara komputasi.
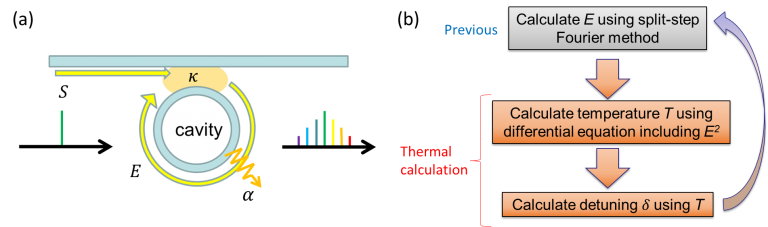
Gbr. 1. (a) Ilustrasi model rongga WGM yang digabungkan. (b) Skema untuk mensimulasikan pembangkitan sisir Kerr dengan efek termal.
Gbr. 1(a) menunjukkan model yang digunakan untuk menghitung pembangkitan karcis optik. Ketika cahaya dimasukkan dari pandu gelombang ke resonator melingkar, sebuah karcis optik dihasilkan di dalam resonator. Karena efek termal tidak diperhitungkan dalam metode perhitungan sebelumnya, model perhitungan baru yang menggabungkan efek termal dibuat dengan menambahkan prosedur perhitungan yang ditunjukkan pada Gbr. 1(b).
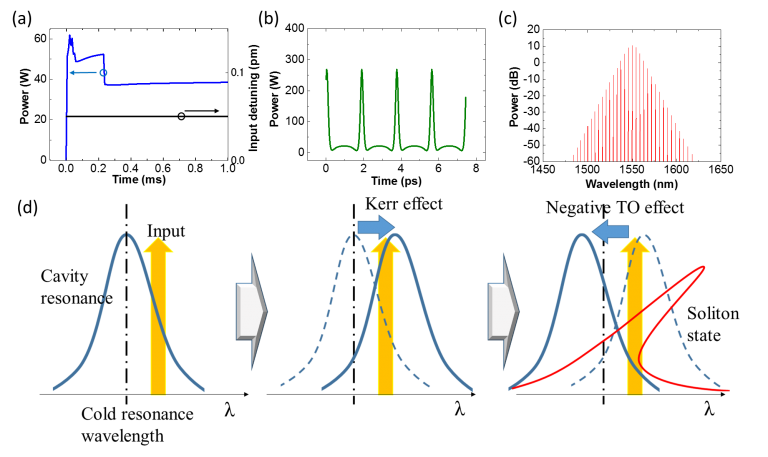
Gbr. 2 (a) Daya intrakavitas (garis biru) dan detuning input dari resonansi rongga dingin (garis hitam), dihitung dengan CaF2 (b,c) Bentuk gelombang temporal dan spektrum optik sisir Kerr di dalam rongga untuk keadaan akhir yang stabil (kesetimbangan termal). (d) Ilustrasi mekanisme transisi ke keadaan soliton yang disebabkan oleh efek TO negatif.
Gbr. 2(a) menunjukkan sebuah CaF2Hasil perhitungan ditunjukkan apabila resonator digunakan sebagai model. Gbr. 2(a) menunjukkan bahwa intensitas cahaya meningkat dengan cepat setelah input cahaya pada 0 ms, kemudian menurun dan bertransisi ke kondisi stabil. Gbr. 2(b,c) menunjukkan bentuk gelombang waktu cahaya dalam resonator dan spektrum cahaya dalam kondisi stabil akhir ini. Hasil ini menunjukkan bahwa pulsa curam (soliton optik) dihasilkan dalam resonator dan spektrum memiliki bentuk sisir yang bersih. Mekanisme ini ditunjukkan pada Gbr. 2(d). Pertama, ketika panjang gelombang yang dekat dengan panjang gelombang resonansi dimasukkan, cahaya terkurung di dalam resonator dan intensitasnya meningkat dengan cepat. Hal ini menyebabkan panjang gelombang resonansi bergeser ke sisi panjang gelombang yang lebih panjang karena efek Kerr optik. Panas kemudian dihasilkan karena penyerapan cahaya, dan panjang gelombang resonansi bergeser ke sisi panjang gelombang yang lebih pendek karena efek termo-optik negatif. Perubahan panjang gelombang resonansi akibat efek termo-optik ini secara praktis setara dengan mengubah panjang gelombang input ke sisi panjang gelombang yang lebih panjang, yang merupakan metode pembangkitan soliton yang dikenal, dan merupakan prinsip di balik pembangkitan soliton.
Pencapaian ini menunjukkan bahwa soliton dapat dihasilkan secara otomatis tanpa mengubah panjang gelombang input sumber cahaya, seperti yang dilakukan secara konvensional, dan diharapkan menjadi salah satu cara yang lebih sederhana dan praktis untuk menghasilkan karcom optik.
- Kategori
- 研究トピックス



