Analyse de l'effet des résonateurs de forme polygonale sur les valeurs Q.

2013-08-09 2022-09-23 miyahara

Recherche

2013-08-09

Vers l'optimisation des résonateurs micro-optiques à haute valeur Q.

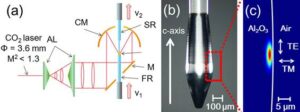
Afin d'obtenir un meilleur confinement optique dans les micro-résonateurs optiques, l'attention s'est portée sur la fabrication de résonateurs optiques utilisant des matériaux cristallins avec une absorption optique plus faible. Le laboratoire Tanabe a mis au point une méthode permettant de fabriquer directement des résonateurs optiques à l'aide d'une technique de croissance cristalline appelée méthode du socle de fusion laser, mais il est apparu que la forme de la section transversale était polygonale. Dans cette étude, le laboratoire Tanabe a analysé la manière dont les valeurs de Q des modes dans les résonateurs polygonaux passent de la forme circulaire à la forme hexagonale, et a précisé les directives permettant d'obtenir des valeurs de Q plus élevées. Nous nous sommes concentrés sur deux modes, le mode perturbé de la galerie de chuchotement (WGM) et le quasi-WGM (Fig. 1(a) et (b)) : le WGM perturbé est un mode qui orbite autour du résonateur avec une réflexion totale le long de ses côtés, tandis que le quasi-WGM est un mode de réflexion totale. mode dans lequel une réflexion totale se produit sur chaque face du polygone.
Pour ces deux modes, le rayon de courbure r des coins du résonateur hexagonal a été utilisé comme paramètre dans l'analyse.

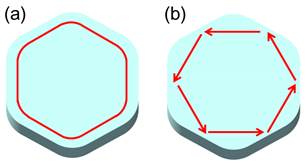
Fig. 1 (a) Mode galerie de chuchotement perturbé.(b) Mode quasi-galerie de chuchotement.

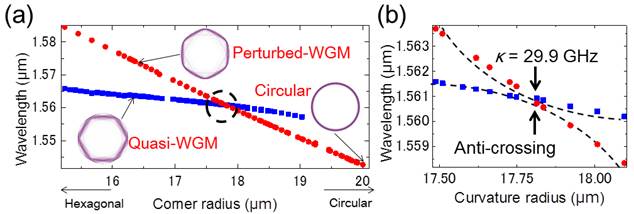
Lorsque l'on fait varier l'arrondissement des coins, les longueurs d'onde de résonance du WGM perturbé et du quasi-WGM changent, mais les deux modes se croisent aux alentours de r = 17,7 μm en raison des différents taux de changement (figure 2(a)). Lorsque le point de croisement est agrandi (Fig. 2(b)), les deux pics spectraux s'avèrent être anti-croisés, indiquant que les deux modes sont fortement couplés.

Fig. 2. (a) Variation de la fréquence centrale en fonction de la rondeur du coin (rayon de courbure du coin).
(b) Vue agrandie de l'intersection du WGM perturbé et du WGM de Quai, où l'intervalle de mode entre les deux est de 29 GHz.

Ce couplage fort limite l'existence indépendante des valeurs Q des deux modes, comme nouvellement découvert dans cette étude. Le résultat est le graphique du rayon de courbure angulaire en fonction de la valeur Q présenté à la figure 3. Même dans les Quasi-WGM, qui sont censés être insensibles à r, la valeur Q chute de manière similaire à celle des WGM perturbés lorsque le résonateur est structuré de manière polygonale par le couplage de deux modes (en fait, il existe d'innombrables couplages de modes).

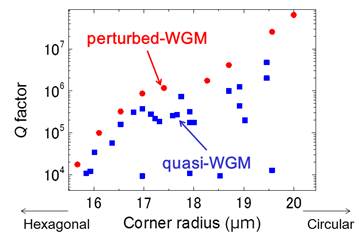
Fig. 3 : Valeurs Q pour le rayon de courbure des coins du MGP perturbé et du quasi-GP.

Nous avons cherché à savoir si des modes à haute valeur Q peuvent également exister dans des structures polygonales et avons constaté que la structure du résonateur doit essentiellement être circulaire pour obtenir des valeurs Q élevées. Nous avons donc développé une méthode de préchauffage pour obtenir un axe cristallin permettant la croissance du cristal en forme circulaire. Nous avons également réussi à obtenir une bonne forme circulaire et à améliorer la valeur du Q.

Une partie de cette recherche a été financée par le programme de promotion de la R&D en matière d'information stratégique et de communications (SCOPE). Il a également bénéficié du soutien financier du Fonds de recherche scientifique et technologique (2560018) et du programme de promotion des projets de recherche de nouvelle génération de l'université de Keio. Les résultats de cette recherche ont été publiés dans Physical Review A 88, 023807 (2013).

Catégories: 研究トピックス

Analyse de l'effet des résonateurs de forme polygonale sur les valeurs Q.

Fabrication de micro-résonateurs optiques à l'aide de techniques de croissance cristalline.

Conférence sur la photonique de l'IEEE Tomohiro Tetsumoto