Analysis of the effect of polygonal shape resonator on Q-value

2013-08-09 2022-09-23 miyahara

Research

2013-08-09

Toward Optimization of High-Q Micro Optical Resonators

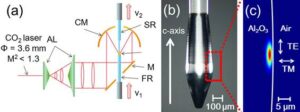
In order to achieve better optical confinement performance in micro optical resonators, attention has focused on fabricating optical resonators using crystalline materials with smaller optical absorption. Tanabe Laboratory has developed a method to fabricate optical resonators directly using a crystal growth technique called laser fusion pedestal method, but it has been found that the cross-sectional shape of the resonators is polygonal. In this study, Tanabe Lab analyzed how the Q-values of the modes in polygonal resonators change from circular to hexagonal, and clarified the guideline for obtaining higher Q-values. We focused on two modes, the perturbed-whispering gallery mode (WGM) and the quasi-WGM (Fig. 1(a) and (b)). mode is a mode in which total reflection occurs on each polygonal surface.
For these two modes, the radius of curvature r of the corners of the hexagonal resonator was used as a parameter in the analysis.

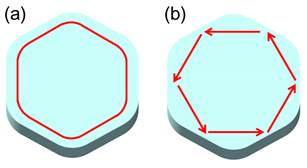
Fig. 1 (a) Perturbed whispering gallery mode. (b) Quasi whispering gallery mode.

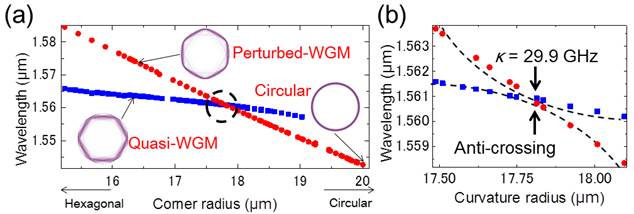
When the roundness of the corners is changed, the resonance wavelengths of the perturbed-WGM and the quasi-WGM change, but the two modes cross at around r=17.7 μm because of the different rates of change (Fig. 2(a)). When the crossing point is enlarged (Fig. 2(b)), the two spectral peaks are found to be anti-crossing, indicating that the two modes are strongly coupled.

Fig. 2. (a) Variation of the center frequency as the roundness of the corners (radius of curvature of the corners) is varied.
(b) Enlarged view of the intersection of Perturbed-WGM and Quai-WGM, where the mode interval between the two is 29 GHz.

We have newly discovered that this strong coupling restricts the independent existence of the Q values of the two modes. The result is the graph of Q-value versus radius of curvature of the corner shown in Fig. 3. Even in Quasi-WGM, which is expected to be r-insensitive, we found that when the resonator is polygonally structured by the coupling of two modes (in fact, there are countless mode couplings), the Q-value decreases similarly to that of perturbed-WGM.

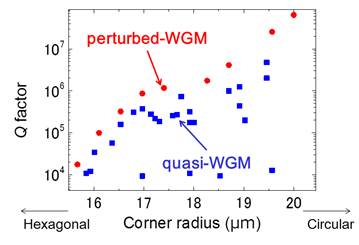
Fig. 3: Q-values versus radius of curvature of the corners of the Perturbed-WGM and quasi-WGM.

We investigated whether high Q-value modes can exist in polygonal structures, and found that the resonator structure must be essentially circular in order to obtain high Q-values. We developed a preheating method to obtain a crystal axis that allows the crystal to grow in a circular shape, and succeeded in obtaining a good circular shape and improving the Q-value.

Part of this research was funded by the Strategic Information and Communications R&D Promotion Program (SCOPE). The research was also financially supported by Grant-in-Aid for Scientific and Technological Research (2560018) and the Next Generation Research Project Promotion Program of Keio University. The results of this research have been published in Physical Review A 88, 023807 (2013).

Categories: 研究トピックス

Analysis of the effect of polygonal shape resonator on Q-value

Fabrication of micro optical resonators using crystal growth technology

IEEE Photonics Conference Tomohiro Tetsumoto