Fast Q-value calculation method for 2-D photonic crystal resonators
Research
Fast Q-value calculation method for 2-D photonic crystal resonators
Development of algorithms with a view to automatic optimization of the structure
Two-dimensional photonic crystal (2D-PhC) resonators are optical resonators with high Q-values that can be fabricated using silicon processes, and are expected to be used in optical devices such as optical switches and memories. When designing resonators, electromagnetic field analysis using the three-dimensional time-domain difference (3D-FDTD) method is used to analyze the resonance wavelength and Q-value, which is known to consume a large amount of computational resources. In this research, we have developed an algorithm that enables faster calculation of Q-values, which is particularly computationally time-consuming.
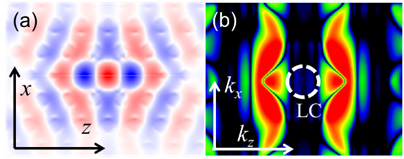
Since the 2D-PhC resonator confines light perpendicular to the slab by total reflection, light in the resonator mode that cannot satisfy the total reflection component radiates out of the slab, limiting the Q-value of the resonator. The wavenumber region that does not satisfy the total reflection condition, where |k⊥|<ω0/c (k⊥ is the in-plane wavenumber and ω0 is the resonance angular frequency), is called a light cone (LC) in the wavenumber space (Figure 1(b)). The Q value can be calculated by determining the Fresnel reflectance and the number of reflections per unit time for each wavenumber component in the LC.
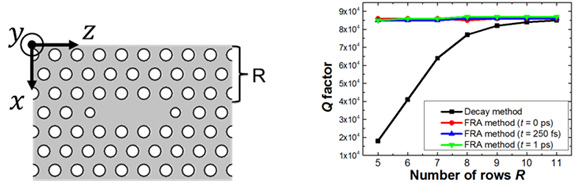
The algorithm was applied to the L3 resonator to calculate the Q-value. The structure is shown in Figure 2. The spacing is 420 nm, the radius is 115.5 nm, the slab thickness is 210 nm, and the vacancies at the sides of the resonator are shifted outward by 32 nm, resulting in a radius of 63 nm. The resonance wavelength for this structure was 1572 nm. The Q-values calculated by the conventional method and the new algorithm based on the energy decay in the computational domain are shown in Figure 3. The mode distributions at 0 s, 250 fs, and 1 ps after excitation were used in the calculation. The number of layers R is the number of vacancies between the resonator and the computational domain. Figure 3 shows that Q values can be obtained accurately using only the data immediately after the end of the source, even when the computational domain is reduced. Similar results were obtained for a width-changing resonator with Q > 107.
The algorithm was shown to significantly reduce both the computational domain and computational steps, reducing the computation time by a maximum of 94%. In the future, we plan to use this method to automatically optimize the 2D-PhC resonator for higher Q-values.
English 
日本語 
简体中文 
Deutsch 
Français 
한국어 
Español 
Italiano 
العربية